乱流の中に確率カオスを発見 —複雑な非線形現象の簡明な記述に成功し,実験系で検証。気象現象や経済現象の予測,解明にも期待—

掲載日：2017-07-13

知能数理研究分野

研究成果のポイント

気象現象などにみられる乱れた旋回流の運動を3変数の確率微分方程式で記述することに成功。
実験データから運動の構造を同定する方法を開発。
ノイズの加わった力学系で生じる確率カオスという現象の存在を理論・実験で実証。

研究成果の概要

北海道大学電子科学研究所(所長,中垣俊之教授)附属社会創造数学研究センターの佐藤讓准教授は,フランス国立科学研究センター(CNRS)の研究者らと共同で乱流旋回流^*1の運動の中に確率カオス^*2を発見し,ランダム力学系^*3理論によりその生成メカニズムを明らかにしました。本研究は,科学研究費補助金基盤研究(C),「雑音誘起現象へのランダム力学系アプローチ」, London Mathematical Laboratory External Fellowship, European Research Council などの支援を受けて実施されました。

論文発表の概要

研究論文名	Stochastic Chaos in a Turbulent Swirling Flow(乱流旋回流の確率カオス)
著者	Divide Faranda¹, 佐藤讓², Brice Saint-Michel^1,3, Cecil Wiertel¹, Vincent Padilla¹, Bérengère Dubrulle¹, François Daviaud¹ (¹フランス国立科学研究センター, ²北海道大学電子科学研究所, ³リヨン大学)
公表雑誌	Physical Review Letters
公表日	米国東部時間 2017 年 7 月 7 日(金)(オンライン公開)

研究成果の概要

背景

米国の気象学者エドワード・ローレンツ博士は,1963年に3変数の方程式に簡約された気象のモデル方程式を数値解析していた際,最初に与えた状態のわずかな違いによって将来の振る舞いが大幅に変わってしまうという予測不可能な運動のメカニズム,「初期値鋭敏性」を見つけました。これは,決定論的カオス^*4と現在呼ばれている現象です。ローレンツ博士の発見した初期値鋭敏性は「バタフライ効果」ともよばれ,「ブラジルの1匹の蝶のはばたきが,テキサスで竜巻を引き起こす」という比喩とともに,小さな揺らぎが将来の出来事を大きく変えてしまう効果として広く知られています。さらにローレンツ博士は,気象が予測不可能である理由を,モデル方程式(ローレンツ方程式)の解であるストレンジ・アトラクター^*5という幾何構造に求めました(図1左)。それ以来,この蝶のような形の解を数学的に研究することにより,古典的なニュートン力学に代表される決定論的方程式であっても予測不可能な運動が生じるメカニズムが明らかにされてきました。

研究手法

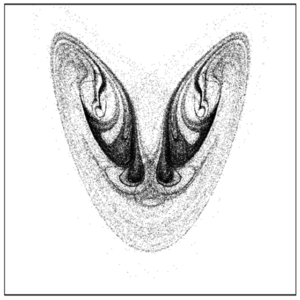
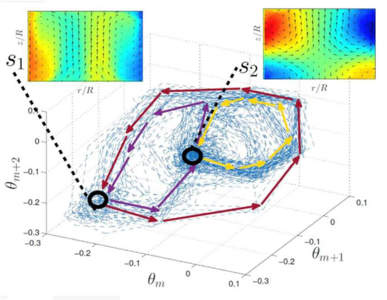
代表的な旋回流系であるカルマン旋回流の高精度実験を,フランス国立科学研究センターのグループが実施しました。この実験では,円柱容器の中の流体をプロペラで撹拌したときに生じる旋回流の運動を観測します(図2左)。佐藤准教授は,この実験で得られた時間とともに変化する膨大なデータに対して,順番に3点ずつペアにして括る「遅延座標埋め込み法」とよばれる解析法を適用することにより,ある幾何構造を見出しました(図2右)。さらに,旋回流で生じる不規則運動を確率変数を含む強制振動方程式である確率ダフィング方程式でモデル化し,「数値安定性解析法」などを適用することにより,この確率微分方程式の定常解であるランダム・ストレンジ・アトラクター^*6(図1右)が,実験データで見つかった幾何構造と定性的に一致するという結論を導きました。このようにして,理論解析結果と実験結果がどちらも,確率カオスを生成するランダム・ストレンジ・アトラクターの存在を示すことがわかりました。

研究成果

佐藤准教授らの研究グループは,ローレンツ博士と同じ考え方に基づきつつも,確率変数を含むランダム力学系モデルを乱流旋回流に対して構成しました。乱流の持つ高次元性を確率変数で表すことにより,複雑な現象をわずか3変数の確率微分方程式で記述することに成功しました。さらに得られたモデルの数値計算結果と実験データを解析して,ノイズの加わった力学系で生じる初期値鋭敏性を発見し,確率カオスという普遍的な現象の存在を理論と実験の両面から実証しました。

今後への期待

今回の研究成果により,ランダム・ストレンジ・アトラクターによって生成される確率カオスという普遍的な現象が,乱流や気象現象のみならず,その他の大規模な非線形現象にも見出されていく可能性が高まりました。様々な大規模な非線形現象のランダム力学系理論に基づく分析や,実験時系列からの高精度のモデル抽出法,その予測制御の解析により,非線形複雑系の数理科学が深化されていくことが見込まれます。さらに,ここで提案された研究手法は,これまで困難だった気象の長期予測への貢献のみならず,経済変動や環境変動の予測など,社会,経済,環境の問題を解明する新たな解析法となることが期待されます。

お問い合わせ先

北海道大学電子科学研究所 准教授 佐藤 讓(さとう ゆずる)
TEL:011-706-9453 FAX:011-706-9453
E-mail:ysato@es.hokudai.ac.jp 又は ysato@math.sci.hokudai.ac.jp
ホームページ:http://www.math.sci.hokudai.ac.jp/~ysato/

参考図

図1:ローレンツ方程式のストレンジ・アトラクター(左図)と,それにノイズの加わった確率ローレンツ方程式^{[文献 2]} のランダム・ストレンジ・アトラクター(右図)。

図2:カルマン旋回流実験(左図)の時系列から,遅延座標埋め込み法により3次元空間に再構成されたランダム・ストレンジ・アトラクター(右図)。右上段のカラーパターンは,実験で観測された2通りの平均流れ場。

用語解説

*1 旋回流: ある軸の周りを旋回し,渦の中心方向に速度をもつ流れ。例えば竜巻の中心に巻き込まれる流れは旋回流である。乱れた旋回流を乱流旋回流という。
*2 確率カオス: 確率微分方程式などのランダム力学系で生じる,初期値鋭敏性を持つ運動。ランダム・ストレンジ・アトラクターにより生成される。ノイズの加わった力学系で生じる複雑運動であり,統計的な意味でバタフライ効果を持つ確率過程である。
*3 ランダム力学系: 駆動力として外部ノイズが加わっている力学系。
*4 決定論的カオス: 常微分方程式などの決定論力学系で生じる,初期値鋭敏性を持つ運動。ストレンジ・アトラクターにより生成される。日本の上田睆亮よしすけ博士(京都大学名誉教授)は,1961年にローレンツにさきがけて, 電気回路の周波数引き込み現象の実験でストレンジ・アトラクターを発見している。
*5 ストレンジ・アトラクター: 初期値鋭敏性をもつ決定論力学系の定常解。ある限られた領域内に閉じ込められていながら,二度と同じ点を通らない無限に長い軌道でできている。部分と全体が自己相似的なフラクタルという幾何構造を持つ。
*6 ランダム・ストレンジ・アトラクター: 初期値鋭敏性をもつランダム力学系の定常解。ある限られた領域内に高い確率で閉じ込められている軌道の束でできている。多重のフラクタル構造を持つ。

参考文献

佐藤譲,「ランダム力学系と確率カオス」, 数理科学 2015 年 8 月号, pp.26-31, (2015).
Mickaël Chekroun, Eric Simonnet, Michael Ghil,“Stochastic climate dynamics: Random attractors and time-dependent invariant measures,”Physica, D 240:21, pp, 1685-1700, (2011).

一覧へ戻る