ポイント
- 感染症モデルに基づく予測の不確実性を解明。
- 感染症の流行初期の統計的鋭敏性と動力学的鋭敏性を発見。
- 感染症モデルによる長期予測は注意深くなされるべきであると提言。
概要
北海道大学電子科学研究所(所長 中垣俊之教授)附属社会創造数学研究センターの佐藤 讓准教授は,フランス・CNRSのDavide Faranda博士,メキシコ・UNAMのIsaac Pérez Castillo博士,デンマーク・Copenhagen UniversityのOliver Hulme博士,フランス・Sorbonne UniversitéのAglaé Jezequel博士,イギリス・Imperial College LondonのJeroen Lamb教授,イギリス・London School of EconomicsのErica L.Thompson博士の5カ国7研究者からなる,London Mathematical Laboratoryの国際共同研究チームとともに,感染症流行を記述するSEIRモデル*1の観測データに対する予測結果の鋭敏性を発見し,ランダム力学系*2理論によりそのメカニズムを明らかにしました。さらに,観測データのわずかな誤差が,予測感染者数を百倍近く増幅させることを解明しました。本研究成果により,常にデータ更新がなされ,直近の観測データによりパラメーターが決定される感染症モデルに基づく予測の不確実性が明らかになりました。このモデリング手法と予測の評価法は,実験的に観察されている様々な社会現象を分析する有力な方法となることが期待されます。
本研究成果は 2020年5月19日(火)オンライン公開のCHAOS 誌の巻頭特別論文として掲載され,American Institute of Physics などでプレスリリースされました。
なお,本研究は London Mathematical Laboratory External Fellowship,日本学術振興会科学研究費補助金基盤研究(C)「ランダム力学系理論に基づく確率カオスの現象論とその応用」などの支援を受けて実施されました。
【背景】
新型コロナウイルス感染症の発生以来,世界中の研究者がその広がりの過程を,各地域での過去の感染者数と死亡者数に関するデータから予測しています。このような予測は,公衆衛生当局や政府が直面するリスクに対する意思決定に役立っており,多くの国で政策決定に援用されています。一般にモデリングと予測が誤差を含むデータに基づいてなされる場合,予測誤差が発生します。とくに新型コロナウイルス感染症のデータは世界中の多くの地域で報告基準が異なるため,様々な測定誤差を含んでいます。
では,その予測の不確実性はどの程度のものでしょうか?佐藤准教授は London Mathematical Laboratory の国際共同研究チームとともに,疫学の現象論モデルである SEIR モデルに対して,データの測定誤差や,データに基づくパラメーターの推定が,長期予測へどのように影響するかを明らかにしました。この研究の目的はある特定の感染症の将来の状況を具体的に予測することではなく,感染症モデルに基づく予測の不確実性を,最悪の予測誤差に基づいて解析することにあります。この研究はイギリスにおいて議論された集団免疫政策の妥当性を検証するために進められました。
【研究手法及び研究成果】
感染症の予測には,感染症の広がりの時間発展を捉える物理モデルと感染症の観測データの両方が必要となります。国際研究チームはジョンズ・ホプキンス大学のシステム科学工学センターから提供されたデータ(https://systems.jhu.edu/research/public-health/ncov/ )を使用し,2020年3月4日から3月20日のイギリス,フランス,イタリアの感染者数に関する予測の統計的鋭敏性と動力学的鋭敏性を解析しました。
統計的鋭敏性:
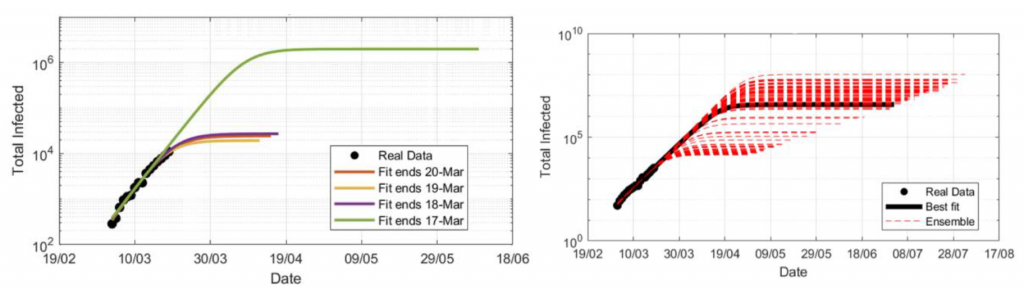
フランスでの流行初期のデータについては,観測期間の開始日を3月4,5,7,10日と変化させても,総感染者数の予測にほとんど影響を与えないことがわかりました。一方で観測期間の終了日を3月17,18,19,20日と変化させると,総感染者数の予測結果は著しく変動しました。3月17日に観測を終了すると予測される総感染者数は約200万人,3月18日に観測を終了すると約3万人となり,推定値に100倍近くの差が生じています (P1図左を参照)。さらに3月20日までのイギリスでの流行初期のデータを使用して,観測終了日の感染者数にノイズを与えた場合に予測がどのように変化するかを解析したところ,観測終了日の感染者数が20%変動すると,総感染者数が5桁増加することがわかりました(P1図右を参照)。以上より統計的予測は,データフィッティングに用いられる最も新しいデータの誤差に極めて敏感であることがわかります。この性質は流行初期で感染者数が指数的に成長するという感染症ダイナミクスの性質に起因します。
動力学的鋭敏性:
ほとんどのモデル研究では,潜伏期間,感染率,回復率などのパラメーター値が固定されています。しかし,実際には都市封鎖の影響や病原体の性質の変化など,多くの要因によってパラメーターが時間変化するため,これは非現実的な仮定です。SEIRモデルは実際の現象を極端に粗視化したモデルであるため,流行初期のデータでモデルのパラメーター値を決定すると,最終状態における様々な予測値が現実と大幅にずれる可能性があります。この問題を解析するために,感染力の指標である実効再生産数*3など,各種のパラメーターを確率変数に置き換えたランダム力学系モデルを構成し,現象として観測されうる全ての可能な軌道のアンサンブルを評価しました。結果として,様々な統計量について,ある特定のパラメーター(例えば感染率など)の変動は最終状態の予測値に大きく影響するが,他のパラメーターの変動は予測値にそれほど影響しない,といった偏向性をもつことがわかりました。また,このような「敏感なパラメーター」が揺らぐと,1日あたりの新規感染者数といった重要な統計量も不規則に変動し,この傾向はその時点での感染者数が多ければ多いほど顕著になることがわかりました。
結果として,流行初期の感染症ダイナミクスは,測定データの誤差に対して,極めて強い統計的鋭敏性と動力学的鋭敏性をもつことがわかりました。こういった予測の不確実性を避けるためには,最新のデータ値を除外したモデルで予測がどのように変化するかを評価する,最新のデータ値にノイズを付加して得られる予測値のアンサンブルを評価する,特定のパラメーターを確率変数に置き換えた確率的ダイナミクスの軌道のアンサンブルに基づいた予測を評価する,といった方法が考えられます。
【今後への期待】
本研究成果により,常にデータが更新され,直近の観測データによりパラメーターが決定される感染症モデルに基づく予測の不確実性が解明されました。提案されたモデリング手法と予測の評価法は,実験的に観察されている様々な社会現象を分析する有力な方法となることが期待されます。
論文発表の概要
| 論文名 | Asymptotic estimates of SARS-CoV-2 infection counts and their sensitivity to stochastic perturbation (SARS-CoV-2感染者数漸近予測の確率的摂動に対する鋭敏性) |
| 著者名 | Davide Faranda1,2, Isaac Pérez Castillo1,3, Oliver Hulme1,4, Aglaé Jezequel1,5,Jeroen Lamb1,6, 佐藤 讓1,7, Erica1,8, (1ロンドン数学研究所, 2 フランス国立科学研究センター, 3メキシコ国立自治大学, 4コペンハーゲン大学, 5ソルボンヌ大学, 6インペリアル・カレッジ・ロンドン, 7北海道大学,8ロンドン・スクール・オブ・エコノミクス) |
| 雑誌名 | CHAOS(非線形物理学の専門誌) |
| DOI | 10.1063/5.0008834 |
| 公表日 | 2020年5月19日(火)(オンライン公開) |
お問い合わせ先
- 北海道大学電子科学研究所 准教授 佐藤 讓(さとうゆずる)
- TEL 011-706-9453
- FAX 011-706-9453
- メール
- ysato(at)es.hokudai.ac.jp
- ysato(at)math.sci.hokudai.ac.jp
- URL http://www.math.sci.hokudai.ac.jp/~ysato/
配信元
北海道大学総務企画部広報課(〒060-0808 札幌市北区北8条西5丁目)
TEL 011-706-2610
FAX 011-706-2092
メール kouhou(at)jimu.hokudai.ac.jp
【用語解説】
*1 SEIRモデル … 集団を感染状態により,感受性保持者(S),感染者(E),発症者(I),回復者(R)の異なるグループに分け,感染症流行が進行するにつれて個体があるグループから別のグループに移動する、という力学系モデル。
*2 ランダム力学系 … 確率微分方程式など,駆動力としてノイズや外力が加わっている力学系。
*3 実効再生産数 … 自然状態で1人の感染者が平均何人に感染させるかを示す値を基本再生産数という。これに対して,感染症流行のある時点における再生産数を実効再生産数という。実効再生産数 は基本再生産数より常に小さく,時点ごとに異なる値となる。










